Comprendre les courbes elliptiques

Les courbes elliptiques sont devenues au fil des années un concept incontournable de la cryptographie asymétrique. Mais au final, elles restent un concept assez obscure pour beaucoup. Que se cache derrière les ECDSA et ECDH pour ne parler que des applications les plus utilisées ?

Avant tout, ces courbes sont des outils mathématiques intéressants. Bien que récentes en cryptographie (introduites en 1985), elles ont déjà été largement étudiées et ont notamment été utilisées par Andrew Wiles dans sa démonstration du grand Théorème de Fermat (vous savez, la fameuse conjecture du magistrat toulousain dont la démonstration ne tenait pas dans la marge).

Leurs propriétés leur donnent un intérêt particulier pour la cryptographie asymétrique et il est désormais normal de voir ces deux acronymes dans les suites de chiffrement proposées : ECDSA et ECDH sont respectivement l’algorithme de signature numérique sur courbes elliptique et l’algorithme d’échange de clés Diffie-Hellman sur courbes elliptiques.

Mais comment l’utilisation de ces courbes elliptiques améliorent-elles la sécurité de ces algortihmes ?

Pour répondre à cette question, comprenons d’abord ce qu’est une courbe elliptique, et quelles sont celles qui sont intéressantes en cryptographie (et pourquoi).

Loin de nous l’idée de faire un cours magistral sur les courbes elliptiques, mais présentons ici rapidement de quoi il s’agit (et nous nous excusons par avance pour les approximations que nous ferons par la suite, l’idée étant de présenter le concept).

Quelques généralités

Une courbe elliptique est comme son nom l’indique une courbe (i.e: un ensemble de point). Elle est régi par une équation de la forme générique (appelée équation de Weierstrass) :
$y^2 + a_1xy + a_3y = x^3+a_2x^2+a_4x + a_5$

Pour ne pas rentrer dans trop de détail, nous allons admettre que les coefficients $a_i$ doivent satisfaire certaines propriétés pour ne pas admettre de singularité (point de doublement ou de rebroussement). C’est à dire que si on écrit l’équation précédente sous la forme d’une équation homogène F(x,y) = 0 alors les dérivées partielles de F ne doivent pas s’annuler simultanément en un point de la courbe.

Dans le cas qui nous intéresse (ie en cryptographie), l’équation précédente peut être simplifiée par changement de variable et on utilise le plus souvent une équation de la forme $y^2 = x^3 + ax + b$ où a et b vérifient $\Delta = 4a^3 + 27b^2 \neq 0$ pour éviter toute singularité. On dit que cette équation est de la forme de Weierstrass simplifiée. (Mais sachez qu’il existe aussi des équations dites de Montgomery ou d’Edward. Parfois, on l’explicite aussi sous sa forme de Legendre, chacune ayant des avantages).

Mais contrairement à ce que leur nom semble indiquer, ces courbes n’ont rien à voir avec des ellipses et peuvent avoir des formes variées comme le montre les exemples ci-après.

Merci GnuPlot

Sur l’image ci-dessus, quelques courbes avec différentes valeurs (a,b) utilisées. Notez que pour (0,0) et (-3,2), les courbes obtenues ne sont pas elliptiques car $\Delta = 0$ . En effet une courbe ne peut pas être elliptique si elle est singulière (comprendre que les dérivés partielles par rapport à x et y ne peuvent simultanement nulle en un point). Géométriquement on peut aussi l’interpréter comme chaque point n’admet qu’une et une seule tangente à la courbe. Si on en revient à nos deux exemples, la courbe $y^2=x^3$ n’admet pas de tangente au point (0,0) On dit que c’est un point de rebroussement et $y^2 = x^3 -3x + 2$ a deux tangentes au point (1,0), on parle alors de point double. On vous laisse vérifier pour les dérivés partielles…

L’intéret des courbes elliptiques est que l’on peut définir une opération que nous noterons + entre des points de la courbe permettant alors de définir un groupe.

– Commutativité P + Q = Q + P
– Associativité P + (Q+R) = (P+Q) + R
– Il existe un élément neutre P + e = e + P = P
– Chaque point a un opposé R + R’ = e

Cette opération est très simple géométriquement :

On définit le résultat de P+Q, en traçant une droite qui passe par P et Q, cette droite coupera la courbe en un troisième point R. On prend alors le symétrique par rapport à l’axe des abscisses et nous obtenons alors un autre point que nous noterons R’ qui est le résultat de l’opération.

Si P = Q, alors on utilise la tangente de la courbe au point P pour remplacer la droite (PQ). Vous voyez maintenant l’importance de l’unicité de la tangente.

Enfin si Q=-P, alors la droite (PQ) est perpendiculaire à l’axe des abscisses et ne coupe pas la courbe en un autre point : on peut imaginer alors que cette droite coupe la courbe en l’infini, on notera ce point 0 et on pose P – P = 0 et ce 0 est l’élément neutre de notre addition sur courbe elliptique.

https://fr.wikipedia.org/wiki/Courbe_elliptique#/media/File:ECClines-2.svg

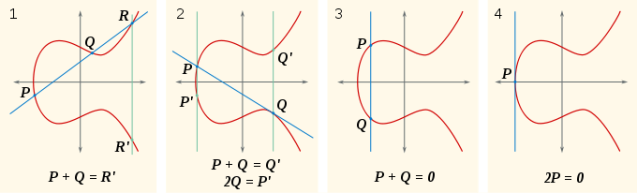
Merci Wikipedia

Cette méthode géométrique est certes pratique mais admet quelques limites. Nous devons donc définir ces opérations sous forme algébrique :

Notons $(x_P,y_P)$ et $(x_Q,y_Q)$ , les coordonnées des points P et Q.

Les coordonnées de S = P + Q sont données par les formules suivantes :

$x_S = m^2 -x_P-x_Q$ et $y_S = m(x_P-x_S) -y_P$

Si P = Q et si $y_p \neq 0$ latex m = \frac{(3x_P^2 + a)}{2y_P}$
Sinon $m = \frac{(y_Q-y_P)}{x_Q-x_P}$

Application à la cryptographie

En général, les courbes elliptiques sont définies sur des espaces continues : par exemple toutes les valeurs sont sur R (l’ensemble des réels). Mais dans le cadre de leur utilisation en cryptographie (et donc dans la suite de ce texte), on change un peu la donne : on va travailler sur les entiers modulo un nombre premier.

Du coup, la représentation de la courbe n’existe plus vraiment en tant que telle : on parle plutot de nuage de point. L’exemple ci-dessous montre la même courbe ( $y^2 =x^3 -3x$ ) representée sur l’espace des réels puis sur les entiers modulo 7 et 23 :

Sur les réels

Sur les entiers modulo 7

Sur les entiers modulo 23

Vous en conviendrez difficiles de remarquer qu’il s’agisse de la même courbe représenter sur des corps différents. Notez au passage que la symétrie est respectée.

La propriété de groupe entre les points est bien entendu préservée. La différence est que nous avons maintenant un groupe cyclique : si nous multiplions un point par 2, puis 3, puis 4, etc Nous finirons par retomber sur notre point.

Cela n’est pas sans rappeler la propriété de $\mathbb{Z}/p\mathbb{Z}*$ avec p premier, où l’on sait d’après le petit théorème de Fermat que pour tout élément $a \in [1;p-1]$ : $a^p = a \mod p$

On dit alors que l’ordre du groupe $\mathbb{Z}/p\mathbb{Z}*$ est p-1.

Dans notre exemple : pour la courbe $y^2 =x^3 -3x$ et sur les corps choisies (ie $\mathbb{Z}_7$ et $\mathbb{Z}_{23}$ ), l’ordre de la courbe (ou encore la cardinalité de la courbe), c’est à dire le nombre de points distinct de la courbe est respectivement égale à 8 et 24 : Soit le nombre de point de la courbe + l’élément neutre à l’infini (souvent noté (0,0,1)).

On pourrait donc croire à tort que l’ordre est toujours p+1.

Bien au contraire, l’ordre de la courbe modulo p est quelque chose de difficile à appréhender car sa valeur n’a rien de systématique. Le théorème de Hasse démontre que l’ordre d’une courbe elliptique est toujours compris entre $p+1+2\sqrt{p}$ et $p+1 - 2\sqrt{p}$ . Mais rassurez vous, nul besoin de compter le nombre de points pour obtenir l’ordre d’une courbe elliptique, l’algorithme de Schoof est là pour vous.

Si nous insistons sur le sujet, c’est que l’ordre d’une courbe elliptique est un critère important de sa sécurité, tout comme la friabilité d’un nombre premier peut l’être pour RSA.

ECDLP

Pour comprendre pourquoi, penchons nous sur l’ECDLP ou en bon français le problème du logarithme discret sur courbe elliptique. Toute la cryptographie sur courbes elliptiques est basée sur ce problème qui est bien similaire à son homologue sur les entiers.

Ici, étant donnés deux points P et Q de la courbe, la difficulté est de retrouver le nombre k tel que Q = kP.

Ainsi l’algorithme d’échange de clé de Diffie-Helman devient :

Arnaud et Bernard (oui, marre d’Alice et Bob) s’accordent sur une courbe et un point G de la courbe.
Arnaud choisit aléatoirement $d_A$ et calcule $G_A = d_A G$ et l’envoie à Bernard.
Bernard choisit aléatoirement $d_B$ et calcule $G_B = d_B G$ et l’envoie à Arnaud.
Arnaud calcule alors $S = d_AG_B = d_A d_B G$ et Bernard calcule $S = d_BG_A = d_A d_B G$ .

Rien de plus. ECDH est considéré aussi dur que ECDLP (de la même façon que la sécurité de DH classique est basée sur la difficulté à résoudre le DLP).

Quelques écueils à éviter :

La Friabilité de l’ordre de la courbe

Comme nous l’avons vu, la difficulté de ECDLP est basée sur la difficulté a retrouvé un nombre k tel que Q = kP. Si l’ordre de la courbe est petit (ou ne possède que des petits facteurs premiers), il sera alors (plus) facile de retrouver ce nombre k.

En pratique dans la vraie vie, les corps utilisés sont d’un ordre de grandeur d’au moins 128 bits, mais dans notre exemple prenons le corps $\mathbb{Z}_{727}$ et choisissons deux courbes E(-3,4) ( $y^2 = x^3-3x+4$ ) et E(-3,0) ( $y^2 = x^3-3x+4$ ). Les deux courbes semblent proches (seul le paramètre b change).

E(3,4)

E(3,0)

Cependant la première a un ordre de 734 (2 x 367) et la seconde a un ordre de 728 (8 x 7 x 13). Cela a un impact significatif sur l’usage de la courbe en cryptographie. En effet nous utilisons la seconde courbe pour effectuer du Diffie-Helmann et que nous choisissions mal notre point G de départ, il pourrait être dans un sous-groupe d’ordre 7 ou 13, permettant alors une brute force alégé pour l’attaquant. Le code ci dessous explicite avec un point de la courbe à l’aide du logiciel sage (apt-get install sagemath) :

sage: Z = Zmod(727)
sage: E = EllipticCurve(Z, (-3,0))
sage: P = E(683, 340)
sage: P.order()
7
sage: P, 2*P,3*P,4*P,5*P,6*P,7*P,8*P
((683 : 340 : 1),
 (326 : 254 : 1),
 (491 : 531 : 1),
 (491 : 196 : 1),
 (326 : 473 : 1),
 (683 : 387 : 1),
 (0 : 1 : 0),
 (683 : 340 : 1))

Dans notre example, il est assez facile de voir que l’ordre est friable car le nombre de départ est petit et nous pouvons aisément le factoriser. Mais si nous avons des ordres de 256 bits; cela devient beaucoup moins trivial de déceler la présence d’un facteur de quelques dizaines de chiffres.

Attaque sur le temps d’éxécution de la multiplication d’un point

Comme nous l’avons vu, le principe du ECDLP repose sur la multiplication d’un point G de la courbe par un scalaire k secret.

Cette opération peut être réalisé de façon basique en additionnant k fois le nombre G

$kG = G + G + \ldots + G$

Mais nous pouvons être plus rapide et réduire le nombre d’opération en décomposant k en puissance de 2. Par exemple si k = 18, au lieu de faire 18 additions successives, nous pouvons obtenir le résultat en 5 opérations en remarquant que 18 = 16 + 2 :

$2G = G + G$
$4G = 2G + 2G$
$8G = 4G+4G$
$16G = 8G + 8G$
$18G = 16G + 2G$

Cependant nous avons aussi vu l’opération d’un doublement d’un point et celle de l’addition de deux points variaient : la constante $m$ n’est pas la même.

Une attaque par canaux auxiliaire consiste à mesure le temps des différents calculs pour (et en déduire s’il s’agit d’un doublement ou d’une addition) et ainsi réduire le champs des valeurs possibles du scalaire k.

Heureusement, certains mathématiciens ont pensé à ce problème et proposé les fameuses équations d’Edwards (dont nous parlions plus haut) : $x^2 + y^2 = 1 +dx^2y^2$ . Ces courbes sont elliptiques sous la condition que $d^5 \neq d$. Mais leur intéret que l’opération de doublement d’un point ou de somme de deux points distincts est identique. Nous vous laissons lire cette présentation pour vous en convaincre pleinement.

Le paramètre b

Bien que les attaques par canaux auxiliaires soient bien connues, en pratique peu de courbes sont de la forme d’Edwards et les courbes les plus utilisées sont de la forme de Weierstrass simplifiée. Il ne vous aura pas échappé que dans le calcul d’un point (doublement ou addition de deux points disctints) la variable b n’est jamais utilisée. L’idée de cette attaque est d’utilisé une courbe avec un ordre friable qui varie d’un facteur b par rapport à une courbe sûre.

Si l’hôte distant ne vérifie pas que le point est sur la bonne courbe, nous pouvons par essaie successif et en utilisant le théorème des restes chinois (encore lui) retrouver le secret de notre victime.

L’idée est alors la suivante :

Bernard et un attaquant se sont mis d’accord sur une courbe $y^2 = x^3 + ax+b$
L’attaquant propose d’utiliser le point G
Bernard pas méfiant utilise le point G et son secret $S_B$ afin de renvoyer $S_BG$

Ce que Bernard ignore, c’est que G n’est pas sur la courbe retenue mais sur la courbe $y^2 = x^3 + ax+b'$ qui a un ordre friable (comprendre plein de petit facteur). Le point G en question a d’ailleurs un ordre petit.

L’attaquant récupère le point qui est un point valide de sa courbe (en effet nul part dans les calcules le coefficient b n’est utilisé) et rapidement obtient une équation $C_1 = S_B \mod N_1$

L’attaquant réitère l’opération avec à chaque fois un point G d’ordre différent.

Au bout du compte, l’attaquant obtient un système d’équation :

$C_1 = S_B \mod N_1$
$C_2 = S_B \mod N_2$
$\vdots$
$C_e = S_B \mod N_e$

Ce système lui permet à l’aide du théorème des restes chinois de retrouver le secret $S_B$ de Bernard.

Moralité de l’histoire : Bernard doit toujours vérifier que les points qu’on lui soumet sont bien des points de la courbe.

Pour plus d’information, vous pouvez lire le papier de recherche sur le sujet.

Préparez-vous à l’inconnu !

De façon générale, il faut être très méfiant sur les courbes elliptiques dès lors que les paramètres ne sont pas justifiés de manière claire et détaillée. Il y a déjà le cas de valeurs parachutées qui se sont avérées plus que douteuses par la suite.

Il ne faut pas non plus sous-estimer les attaques non-publiques ou qui pourraient voir le jour prochainement.

Mais alors pourquoi diable utiliser des courbes elliptiques ?

Voici la principale réponse à cette question : les algorithmes sur courbes elliptiques nécessitent pour une sécurité équivalente moins de ressource.

jshmendes@vmhost:~$ openssl speed ecdsap256 dsa2048 rsa2048 rsa4096
                             sign     verify     sign/s verify/s
rsa 2048 bits              0.001124s 0.000033s    889.4  29557.2
rsa 4096 bits              0.008078s 0.000123s    123.8   8129.2
dsa 2048 bits              0.000391s 0.000409s   2554.6   2444.8
256 bit ecdsa (nistp256)   0.0001s   0.0001s    10919.0   8186.3

Notamment la signature est une action beaucoup plus rapide sur les courbes elliptiques et permet de dégager de la ressource pour faire autre chose. Rappelez vous que dans le cas d’une négotiation TLS c’est le serveur qui a le dernier mot sur le choix de la suite cryptographique et il doit aussi effectuer énormement d’opération de signature : Il a donc tout intérêt à choisir un algorithme sur courbes elliptiques.

Bref, on espère avec tout cela que les courbes elliptiques sont des objets moins obscures.

Si vous avez encore des doutes, n’hésitez pas à poser vos questions en commentaire.

	Factorisation par co… dans Vous avez dit Friable ?
	Factorisation par co… dans Comprendre les courbes el…
	Factorisation par co… dans La panne
	Comprendre les courb… dans Petit durcissement de son serv…
	Compression et chif… dans Protection des messages par…